
Nella mia classe prima ho da poco introdotto le potenze; durante la prima lezione abbiamo cercato di fare amicizia con queste moltiplicazioni ripetute con semplici esercizi di lettura e di calcolo.
Durante la seconda puntata abbiamo vivacizzato un po’ la situazione lanciando i dadi, proprio così!

Alla LIM abbiamo proiettato questo sito dove è possibile scegliere dadi in diversi formati e lanciarli per ottenere sempre nuovi esercizi; io ho proposto il dado a 12 facce per la base e il dado a 4 facce per l’esponente, ma dopo un po’ di riscaldamento i ragazzi hanno reclamato l’uso del dado a 20 facce e una sfida finale con esponenti fino al 6.
Per concludere abbiamo colto una sfida dal nostro libro:
Un enorme foglio di carta viene piegato in due. Poi viene nuovamente piegato in due. Quante volte si dovrebbe continuare a piegare a metà il foglio, affinché lo spessore della carta raggiunga l’altezza della Torre di Pisa (56 metri)? Supponi uno spessore della carta di 0,1mm
Contaci! – Zanichelli
Ogni volta che pieghiamo a metà il foglio il numero degli strati raddoppia, quindi si tratta di calcolare le potenze di 2 fino a raggiungere un numero vicino a 560 000. Per un po’ ci siamo affidati alla nostra capacità di raddoppiare, poi ci siamo aiutati un po’ con la calcolatrice per velocizzare i tempi.
Trovata la soluzione (2 alla 19esima) ho chiesto ai ragazzi di sparare una stima:
Quante pieghe dovremmo fare per raggiungere la Luna?
Ognuno ha scritto sul quaderno la propria idea, abbiamo cercato il dato che ci interessava (384.400 km) e nutrito la calcolatrice con le nostre stime. Inutile dire che la poveretta è andata in tilt un sacco di volte, 2 alla 5000esima era davvero troppo per lei!
Con un po’ di pazienza alcuni risultati sensati sono arrivati e siamo inciampati nelle nostre prime notazioni esponenziali.
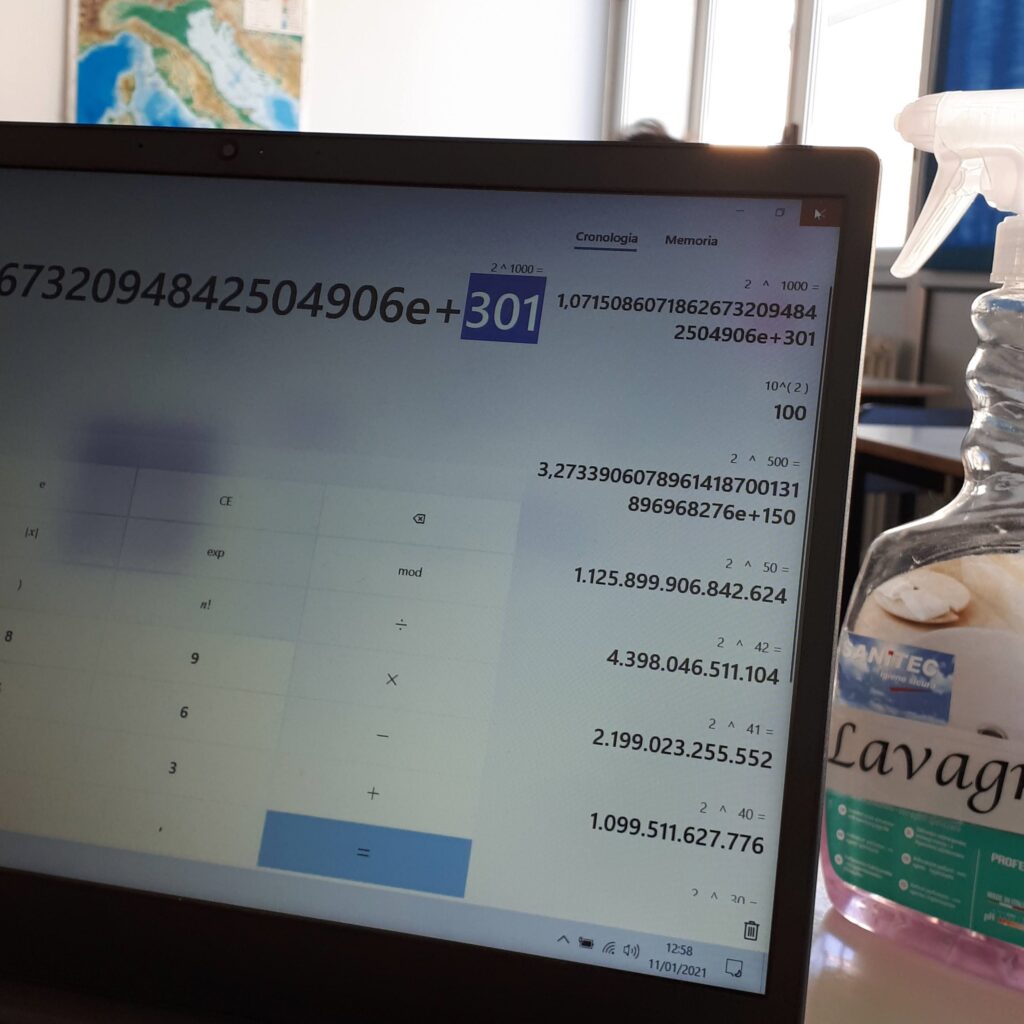
Sorprendentemente bastano “solo” 42 pieghe per raggiungere il nostro amato satellite.
Stanchi, ma soddisfatti delle nostre fatiche ci siamo lasciati con una sfida per casa che tenesse alta la motivazione anche per la volta successiva:
Io sono riuscita a piegare questo foglio bene benissimo soltanto 6 volte, vediamo chi riesce a fare di meglio!

Prof, ma posso usare una pressa?
No! Non vale, ma puoi usare qualunque altra furbizia riproducibile in classe
Eccoli la volta dopo carichi come molle a farmi vedere quante volte sono riusciti a piegare i loro fogli, quasi tutti almeno 7 volte, qualcuno non ha colto che il foglio andava piegato ogni volta a metà producendo oggetti simili a ventagli, ma alcuni sono riusciti a fare un passettino in più, ecco le strategie vincenti:
- Scegliere un foglio più sottile
- Scegliere un foglio più grande
- Scegliere un materiale più elastico della carta
- Piegare molte volte a metà nella stessa direzione per ottenere un rettangolo lungo e sottile da ripiegare a sua volta
Grazie alla segnalazione di un amico ho recuperato un video in cui i famosi MythBusters cercano di piegare un foglio di carta più di 7 volte (limite a cui anche noi siamo giunti con i fogli normali) arrivando addirittura ad 11.
Il video è in inglese, ma ci siamo sforzati di ascoltare almeno i numeri e ad un certo punto è spuntato 1 024: il numero di strati di carta alla decima piega, tantissimi!!
Ebbene, combinando le furbate giunte dalle varie teste pensanti siamo riusciti anche noi a realizzare le famigerate 11 pieghe, ma non ci sembrava affatto che nella nostra pallina di pellicola trasparente ci potessero stare più di 1 000 strati!
Prof, ma è impossibile!
Allora via a riaprire la pellicola e a rifare tutte le pieghe tenendo bene il conto degli strati ad ogni passaggio… 2 048 😱😱😱.
No prof, è davvero impossibile che ci siano duemila strati!
Eh, ragazzi, bisognerebbe tagliare qui con le forbici e contarli uno per uno, non penso che si riesca, si romperebbero le forb….. come non detto!

Prof, guardi! Sono davvero tantissimi
Eh già! La cosa strana delle potenze è che all’inizio sembra che crescano pian pianino, ma ad un certo punto i numeri aumentano così tanto che sfuggono alla nostra comprensione, sembrano esplodere!
Succede così anche con i contagi.
Facciamo una prova: una persona malata ne contagia due:
- 1^ settimana: 2 contagiati
- 2^ settimana: 4 contagiati
- 3^ settimana: 8 contagiati
- 4^ settimana: 16 contagiati
- 5^ settimana: 32 contagiati
- 6^ settimana: 64 contagiati; fin qui sembra di poter stare tranquilli
- 7^ settimana: 128 contagiati; tantini ma gestibili
- 8^ settimana: 256 contagiati; forse è meglio prendere provvedimenti
- 9^ settimana: 512 contagiati; sì, prendiamo provvedimenti
- 10^ settimana: 1024 contagiati; ops sono tantissimi
- 11^ settimana: 2048 contagiati; siamo decisamente nei pasticci!
Da qui abbiamo provato a confrontarci su quale fosse il momento giusto per prendere provvedimenti ed evitare l’esplosione dei contagi.
Se hai trovato utile l’articolo puoi supportare il mio impegno offrendomi un caffè cliccando sul pulsante qui sotto:




